Expected goals (xG) is a huge talking point in the footballing world with many avid football fans using it as a key metric of performance. On X (Twitter), there is an account with half a million followers called the xGPhilosophy. With the huge amount of pressure placed on these players by the fans, the term "expected" goals can sometimes result in overreactions to isolated instances of sub-par performances. As part of my personal project, I wanted to create a resource that helps football fans to visualise how xG is actually calculated.
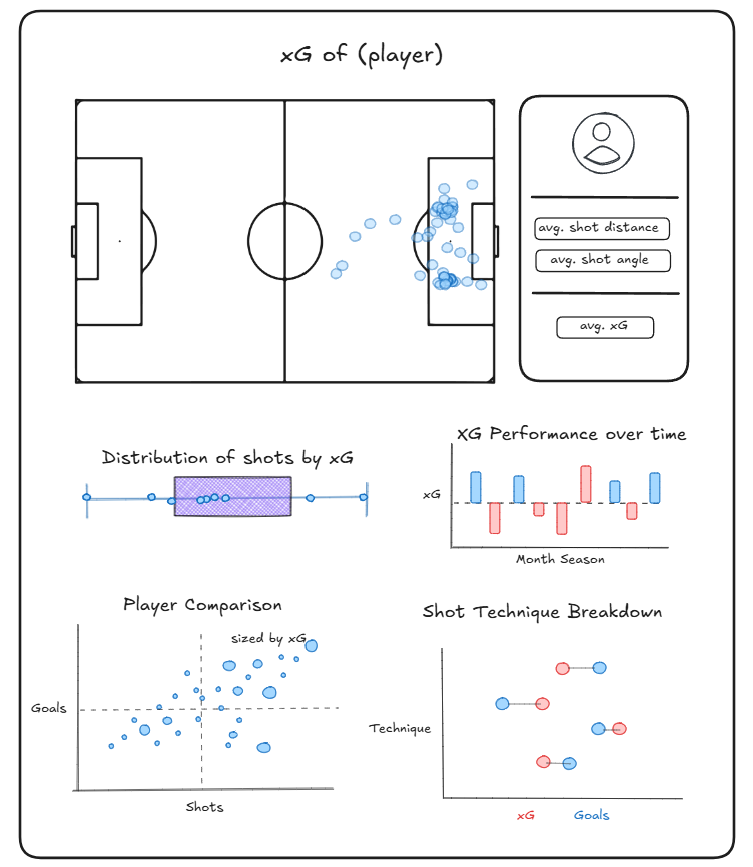
Using the same xG model and calculations a secondary exploratory dashboard can be used to analyse individual player performance. Below is an example of a few charts that accompany a heatmap of shots taken. It should be noted that there are an incredibly large number of factors that affect the result of a shot resulting in a goal. Information about the previous pass prior to the shot is one example, not to mention the impact of defensive players.
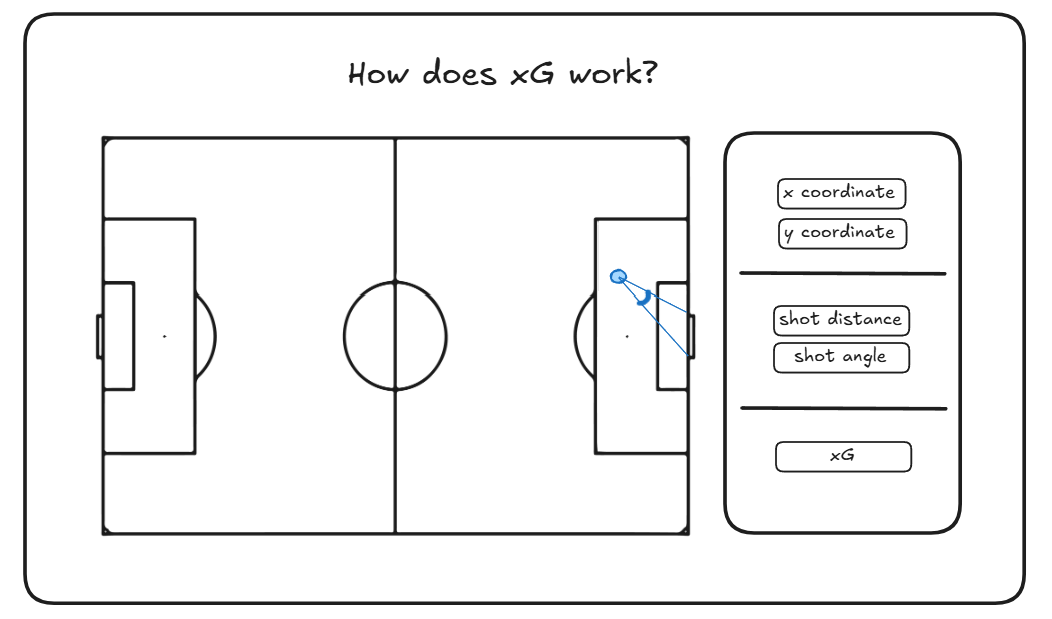
What is xG?
xG can be defined as measuring the quality of a chance by calculating the likelihood that it will be scored by using information on similar shots in the past (Opta). It is measured on a scale between zero and one, with zero representing a chance where scoring is impossible and one representing a chance that is expected to result in a goal every time. Factors such as distance, angle, body part used, and defensive pressure all contribute to calculating the xG of a chance/shot. However, many sources cite distance to goal and shot angle to be two of the most important predictors of goal probability. A simple logistic regression model (Scholtes & Karakus) for calculating xG can be seen below. With this model, we will only be focusing on distance to goal and angle of the shot (for now).
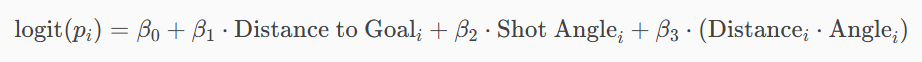
Requirements
For this project we need to:
- Create a coordinates 'scaffold' dataset
- Access historical player data and their shot coordinates
- Map coordinates onto a pitch diagram in Tableau
- Calculate distances and angles using Pythagorean Theorem and trigonometry
- Use model to calculate xG
